Dia Internacional da Lógica

No Im3 continuamos a celebrar o Dia Internacional da Lógica pelo segundo ano consecutivo porque a lógica é simplesmente fantástica.

E continuamos a usar o Teorema de Pitágoras como exemplo por ser paradoxalmente simples e complexo ao mesmo tempo.

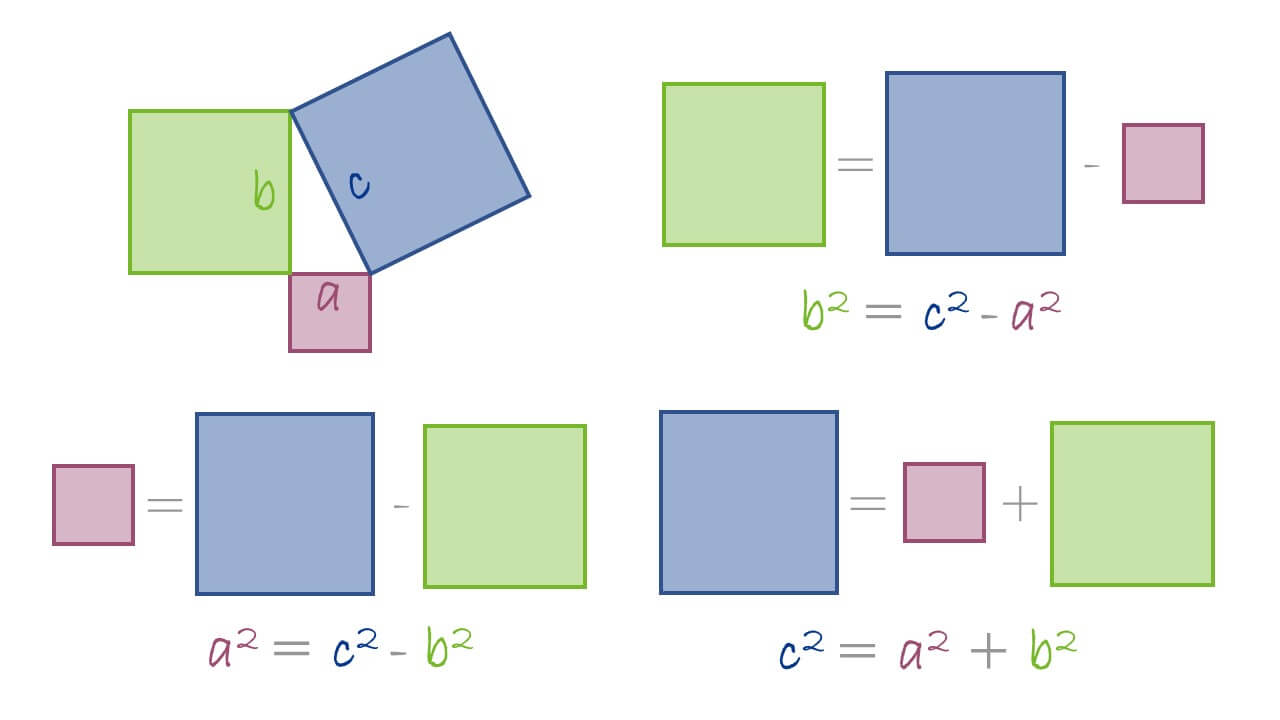
Milhões de pessoas simplesmente olhando longamente para os símbolos e quadrados na imagem acima, sem a necessidade de maiores explicações, poderiam entender o Teorema mais conhecido do mundo, cuja equação a2=b2+c2 rivaliza em fama com a E= mc2 de Einstein.

E ambas as equações compartilham outra característica: uma grande simplicidade que esconde algumas leis fundamentais muito profundas.

Se traçarmos um círculo com centro na interseção b-c e raio igual a c, podemos começar a desenvolver todas as razões e propriedades trigonométricas por dedução e desenvolvimento lógico, até definirmos as formas senoidais com as quais as funções de onda podem ser representadas, que são a maneira mais básica de descrever qualquer objeto em Mecânica Quântica.

As funções senoidais também podem representar a propagação de campos, inclusive o eletromagnético, que se tiverem o comprimento de onda adequado serão visíveis na forma de luz, cuja velocidade é igual a c, constante universal da equação de Einstein que formula a equivalência entre energia E e massa m.

Voltando ao Teorema de Pitágoras, que formulamos em duas dimensões, vale também na sua forma tridimensional, por exemplo, para a superfície de uma esfera como a Terra, vale o seguinte: R2=x2+y2+z2. Em sua Teoria Geral da Relatividade, Einstein acrescentou a dimensão temporal T, validando que a equação x2+y2+z2-T2 é uma versão espaço-temporal quadridimensional do Teorema de Pitágoras.

O que tentamos mostrar neste post é que temos a lógica ao nosso alcance para todos os níveis de dificuldade, do zero ao infinito e além:

“O mundo é simples e complexo, lógico e estranho, ordenado e caótico” Frank Wilczek